Working in Binary, Hexdecimal, Etc.:
bc, gforth, and Other Options
We've started dealing with such things as global constants in memory, and now we find ourselves unable to avoid working with binary numbers and their shorter forms, octal or hexadecimal. For addresses and large numbers, decimal is not nearly as efficient as binary, and almost all modern CPUs (meaning since the 1960s) use binary -- base two.
(There is a lot of stuff I'm sweeping under the rug here. We generally prefer
not to go deep diving in unfamiliar waters.)
All the CPUs we have been talking about so far, and all the ones I am (at this time) considering demonstrating here do their math (and other operations) in binary.
We western earthling humans of the current common cultures do not tend to find it comfortable to operate in binary. Therefore, it would be good to have tools to help us.
Binary may be efficient, but it is very much not a compact way of
writing numbers on paper or in blogs. For example, one million in decimal base
(base ten) is one followed by six zeroes:
1000000ten
But in binary base, it is
11110100001001000000two
Twenty, count them, twenty digits.
In octal base (base eight), it is a more compact seven digits, not quite as
compact as in decimal:
3641100eight
And in hexadecimal base (base sixteen), it is even more compact than in
decimal:
F4240sixteen
-- only five digits.
Converting from binary to octal is rather straightforward. First write the binary number in groups of three digits. Start from the right and go left. The leftmost group need not be a full group of three:
11 110 100 001 001 000 000two
Then convert each of the groups to octal according to the following
table:
| binary | octal | binary | octal | |||
|---|---|---|---|---|---|---|
| 000 | == | 0 | * |
100 | == | 4 |
| 001 | == | 1 | * |
101 | == | 5 |
| 010 | == | 2 | * |
110 | == | 6 |
| 011 | == | 3 | * |
111 | == | 7 |
11 => 3, 110 ~> 6, 100 => 4, 001 => 1, 001 >> 1, 000 => 0, 000 => 0And converting from octal to binary just uses the above table in the opposite direction.
=> 3641100
Converting between binary and hexadecimal is just as straightforward, grouping
the binary digits in groups of four instead of three. Again, the leftmost
group does not have to be full four (although it is for one million):
1111 0100 0010 0100 0000two
Convert by groups according to the following table:
| binary | hex | binary | hex | |||
|---|---|---|---|---|---|---|
| 0000 | == | 0 | * |
1000 | == | 8 |
| 0001 | == | 1 | * |
1001 | == | 9 |
| 0010 | == | 2 | * |
1010 | == | A |
| 0011 | == | 3 | * |
1011 | == | B |
| 0100 | == | 4 | * |
1100 | == | C |
| 0101 | == | 5 | * |
1101 | == | D |
| 0110 | == | 6 | * |
1110 | == | E |
| 0111 | == | 7 | * |
1111 | == | F |
1111=>F, 0100=>4, 0010=>2, 0100=>4, 0000=>0
=> F4240
I know you're hoping for a simple method like this for converting between decimal and binary, but, unfortunately, converting between base ten and base two is not as easy. There is a reason (ten is not an even power of two), but let's not go too far wide in our detour. Not here. It may become more clear when we practice conversion routines, a little down the road.
But it's not exactly hard, if you're okay with doubles and halves in decimal, keep track of evens and odds, and can work from left-to-right and from right-to-left, and keep at least one thing in memory.
Let's try converting a million from decimal to binary.
First, write down a million in decimal, a one followed by six zeroes:
1000000
Is it even or odd? It's even, so the rightmost binary digit is zero:
0
Half of a million is five hundred thousand:
500000
That's even, so the next binary digit is 0:
00
Half of five hundred thousand is two hundred fifty thousand:
250000
Hmm. Let's make this a bit more followable:
| step | decimal | odd? | half | remainder | binary |
|---|---|---|---|---|---|
| 0 | 1000000 | even | 500000 | r 0 | 0 |
| 1 | 500000 | even | 250000 | r 0 | 00 |
| 2 | 250000 | even | 125000 | r 0 | 000 |
| 3 | 125000 | even | 62500 | r 0 | 0000 |
| 4 | 62500 | even | 31250 | r 0 | 00000 |
| 5 | 31250 | even | 15625 | r 0 | 000000 |
| 6 | 15625 | odd | 7812 | r 1 | 1000000 |
| 7 | 7812 | even | 3906 | r 0 | 01000000 |
| 8 | 3906 | even | 1953 | r 0 | 001000000 |
| 9 | 1953 | odd | 976 | r 1 | 1001000000 |
| 10 | 976 | even | 488 | r 0 | 01001000000 |
| 11 | 488 | even | 244 | r 0 | 001001000000 |
| 12 | 244 | even | 122 | r 0 | 0001001000000 |
| 13 | 122 | even | 61 | r 0 | 00001001000000 |
| 14 | 61 | odd | 30 | r 1 | 100001001000000 |
| 15 | 30 | even | 15 | r 0 | 0100001001000000 |
| 16 | 15 | odd | 7 | r 1 | 10100001001000000 |
| 17 | 7 | odd | 3 | r 1 | 110100001001000000 |
| 18 | 3 | odd | 1 | r 1 | 1110100001001000000 |
| 19 | 1 | odd | 0 | r 1 | 11110100001001000000 |
| 20 | 0 | even | 0 | r 0 | 011110100001001000000 |
Okay, that's a bit tedious, but it is straightforward. And the reverse is also
straightforward and a bit tedious. Not hard, but tedious, and easy to get
distracted and make mistakes. (I cheated and used a bit of Forth to
generate the above conversion.)
Since you probably don't find it easy to do the conversions in your head, nor easy to do math in your head in non-decimal base, let's look around for tools to do it for us. (I don't find it all that easy either.)
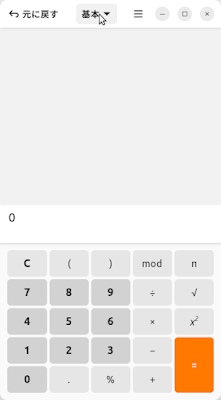
As I mentioned already, your personal workstation, whether it runs a Microsoft OS or a Linux OS or a BSD OS or an Apple OS, or something else, probably comes with a fancy calculator installed. That calculator probably has a programmer mode, and the programmer mode will (usually) have the option to work in binary, octal, and/or hexadecimal, in addition to decimal.
On my current Linux OS desktop (Gnome/Ubuntu from some time back), there is such a calculator, and there is a mode button in the center of the menu/tool bar at top that says "Basic" or something in English. (「基本」 == "kihon" in Japanese. Sorry, but I work in Japanese, my screenshots will be Japanese.)
If you click on 基本 there and select "Programming" or whatever it is (「プログラミング」) it gives a set of programmer-oriented functions:
And then you can select the base. Below, I have selected base 16 (「16 進数」 == "jū-roku shinsū"):
And this calculator does me the convenience of showing me the number I'm entering in binary in that big patch in the center. It also shows whichever of octal, decimal, and hexadecimal I am not entering the number in, over to the right, just below the entry area. Below, I have just typed in one million in decimal, but haven't yet hit the enter key:
I had kind of hoped I could drag-select and copy those displayed conversions, but this version isn't that nice. On the other hand, once I hit the enter key, and the entered number is bolded,
And I can select and copy that number out of the entry window. So it's actually pretty nice after all.
Most modern desktop calculator applications in desktop workstations do something similar for you. You should be able to figure out how after playing around with them for a bit.
So, this is one way to get some help working with hexadecimal and binary, so we don't get too lost in the math.
But there are other options, including programming languages such as Forth and bc. (The interactive modes of Ruby, Python, Pearl, Julia, and many other languages are also useful, but I find Forth and bc particularly helpful to me.)
We'll discuss Forth more a bit down the road, and I don't want to
confuse things with post-fix mathematical expressions and such just now, so
I'll focus on bc.
bc
The Unix "basic calculator", bc, is a part of the usual set of tools for the programmer that works in *nix environments. It's been around since about the time the first Unix systems were called "Unix". It's almost always present on any OS derived from or developed to be compatible with Unix, including the various Berkeley Systems Distributions, Mac OS X and beyond, Linux OSses, Minix, and so forth.
The reason is that system maintenance scripts sometimes need to work with very large numbers, and that's something bc does fairly well and predictably.
It was not, the last time I checked, among the tools available in your standard distribution of Microsoft Windows, but you can get it for MSWindows with Cygwin, as I have mentioned already.
I'm not sure if it is in Microsoft's WSL. I don't go there. It will be in Microsoft's Linux-OS-on-Windows distributions, I'm sure, if you go that direction, since those just basically use the native distribution's repositories. I still recommend Cygwin.
Instructions for installing Cygwin are on the Cygwin site. I may sometime write up a bit more on the ins and outs of that, but I'm focusing on assembly language right now. I strongly recommend checking both the signature and the hash before installing, both of which are noted on the instructions page.
Back to bc.
There are two major versions of bc, one from the GNU tools and the
other from the BSD tools. Aside from the way they start up, for what we will
be using them for here, they are pretty similar. (OpenBSD's
bc is a bit more minimalist than the rest, but I'm assuming if you use
OpenBSD for this project, you'll understand why and what to do about it.)
Invoking bc from the command line is fairly straightforward. Just type "bc" and hit enter. Except that doesn't give you some things I find convenient, so type the "-l" ("--mathlib") option, as well, and bring in some minimal library functions:
$ bc -l
bc 1.07.1
Copyright 1991-1994, 1997, 1998, 2000, 2004, 2006, 2008, 2012-2017 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
The BSD versions are much more quiet on startup. If you don't need the reminders, the GNU versions will be quiet if you give them the "--quiet" or "-q" option.
To quit bc, you can type the "quit" command. (Or you can hit the Ctrl-D
key combination at the beginning of the line, in *nix. I think that will be
Ctrl-Z in MSWindows. End Of File marker.)
I'm not going to give a full introduction to bc here. If you want to
learn more, open a fresh command-line shell terminal window and type "man bc"
to get a look at the on-line manual page. Or look it up on your favorite web
search engine, using, say,
man page bc ubuntu
for your search terms if your OS is Ubuntu.
So, you have started bc in a terminal shell and are wondering what to do next.
For starters, just think of it as a calculator.
The addition operator is what you would expect, "+". Type "8 + 8" and hit the
enter key and it will show you "16":
8 + 8
16
Subtraction is also no surprise, it's the usual hyphen key:
128 - 32
96
Likewise division is the usual slash:
44859318 / 57734
777.00000000000000000000
Multiplication may be a surprise if you haven't done much with computers, but
most likely you've already seen the asterisk as the substitute for the tilted
cross "×", as the multiply operator commonly used today on computers:
4294967295 * 3415927
14671294747107465
Finally, for integer powers only, there is the caret as exponent:
2 ^ 128
340282366920938463463374607431768211456
You can save results in variables:
m = 2^20
and then use them the same as numbers:
32 * m
33554432
Note that when you make an assignment, bc does not print the result.
When you don't, it does.
bc has some internal variables. One is scale, which determines how many decimal places of accuracy to maintain to the right of the decimal point:
scale=102
4*a(1)
3.141592653589793238462643383279502884197169399375105820974944592307\
816406286208998628034825342117067980
Heh. Talk about cheating at calculating π. π here is accurate up to the last two digits, though.
Oh, and when it has to use more than a line for a result, it shows that by putting a backslash at the end of the incomplete line to escape the end-of-line character.
And, uh, yea, the a() library function is the arctangent. (See the man
page.)
Oh, and yeah, that, too, bc operates internally in base ten. LoL. Less
surprise that way.
Another internal variable is obase, which determines the base it converts output to:
obase=2
2^32
100000000000000000000000000000000
obase=16
2^64
10000000000000000
2^64-1
FFFFFFFFFFFFFFFF
You've been wondering when I would get back to binary and hexadecimal, haven't you?
Input base conversion is a separate variable, ibase. That's why we
could still type it in as
obase = 16
up there. Once we start playing with ibase, we need to be more careful,
and write it as something like
obase = 8 + 8
instead.
bc allows C-style comments inside /* ... */ pairs.
obase = 5 + 5 /* Just in case. */
ibase = 8
777 /* Enter at the end of this line produces output. */
511
ibase = 8 + 8 /* Can we do this? Yes, we can. */
F4240 /* Enter at the end of this line produces output. */
1000000
Since we're here, let's check the math we've been having the CPU do:
ibase = obase = 8 + 8
8 + 5
D
8 + 5 + 2
F
8 + 5 + 2 + 7
16
8 + 5 + 2 + 7 + 4
1A
Yep. Checks out.
bc is friendly enough to interpret single digits of 2 to 9 correctly no matter what ibase is, which can be helpful, or can be confusing. But hexadecimal A through F must be upper-case (capital). Lower-case letters are assumed to be variable names.
Now we have two ways to work with hexadecimal and binary numbers.
Try something amusing?
obase = ibase = 5 + 5
obase = ibase = 36
FRIENDS + ENEMIES
30 14 33 01 05 28 20
Okay, didn't work, did it? At least, not the way we thought it would. When obase goes over sixteen, the output is written in groups of decimal numbers instead of using the alphabet after F.
Hmm.
Forth (gforth)
I said I wasn't going to distract you with post-fix math. I lied. :)
If you took my hints and installed gforth, you can follow along. You
can quit out of bc and use the same terminal shell you were running
bc in:
$ gforth
Gforth 0.7.3, Copyright (C) 1995-2008 Free Software Foundation, Inc.
Gforth comes with ABSOLUTELY NO WARRANTY; for details type `license'
Type `bye' to exit
In post-fix, the numbers come first, then the operators.
5 5 + .
The plus is addition, as you suspected. It adds two numbers on the stack and replaces them with their sum. The period (dot) is an operator that takes the top number on the stack and converts and outputs it in the current input/output numeric conversion base.
Hit enter after the dot, and it prints the result, followed by "ok":
5 5 + . 10 ok
You can set a variable with the ! operator. And you can enclose comments in
parentheses.
4 4 * base ! ( Now hexadecimal base. ) ok
1000 F34 + . 1F34 ok
In some ways, not having input base and output base separate is easier than bc. In others, it's messier. But just remember that
10 base !
is always redundant, and doesn't change anything.
5 5 + base ! ( Back to decimal. ) ok
36 base ! ( Now what? ) ok
FRIENDS ENEMIES + . UEX15SK ok
gforth does not do arbitrary precision unless you program it to do so, but, on a 64-bit processor, it can handle a little more than 12 digits of base 36 in integer math.
Okay, that was not necessary, I suppose. :-p
I'll explain more about how to use bc and gforth more when we need them.
For now, play with bc and gforth a little, especially converting some numbers
of your own choice between binary, hexadecimal, and decimal.
And soon it will be time to talk about treating that list of small integers we've been working with as a real list.